Featured image of post DeepLearning Basic
Coding

DeepLearning Basic

不知道大伙有没有感觉到，cursor这东西出来后web开发星人的危机感…这玩意可能要带来生产方式的大变革…尝试布局中

DL basic

感知机->神经网络

感知机的设计思想很像神经网络的雏形。感知机是接收0，1信号，并输出0，1信号的一种处理结构。中间会进行函数运算，如：

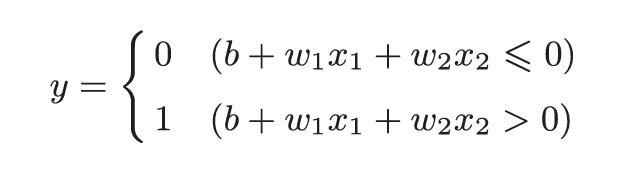
权重w是控制输入信号重要性的参数；偏置b是调整神经元被激活的容易程度。

用感知机能够实现与门，与非门，或门的模拟。

然而，感知机无法实现异或门的输出，其局限性在于它只能表示由一条直线分割的空间。为了实现异或门，我们引入多层感知机：

激活函数

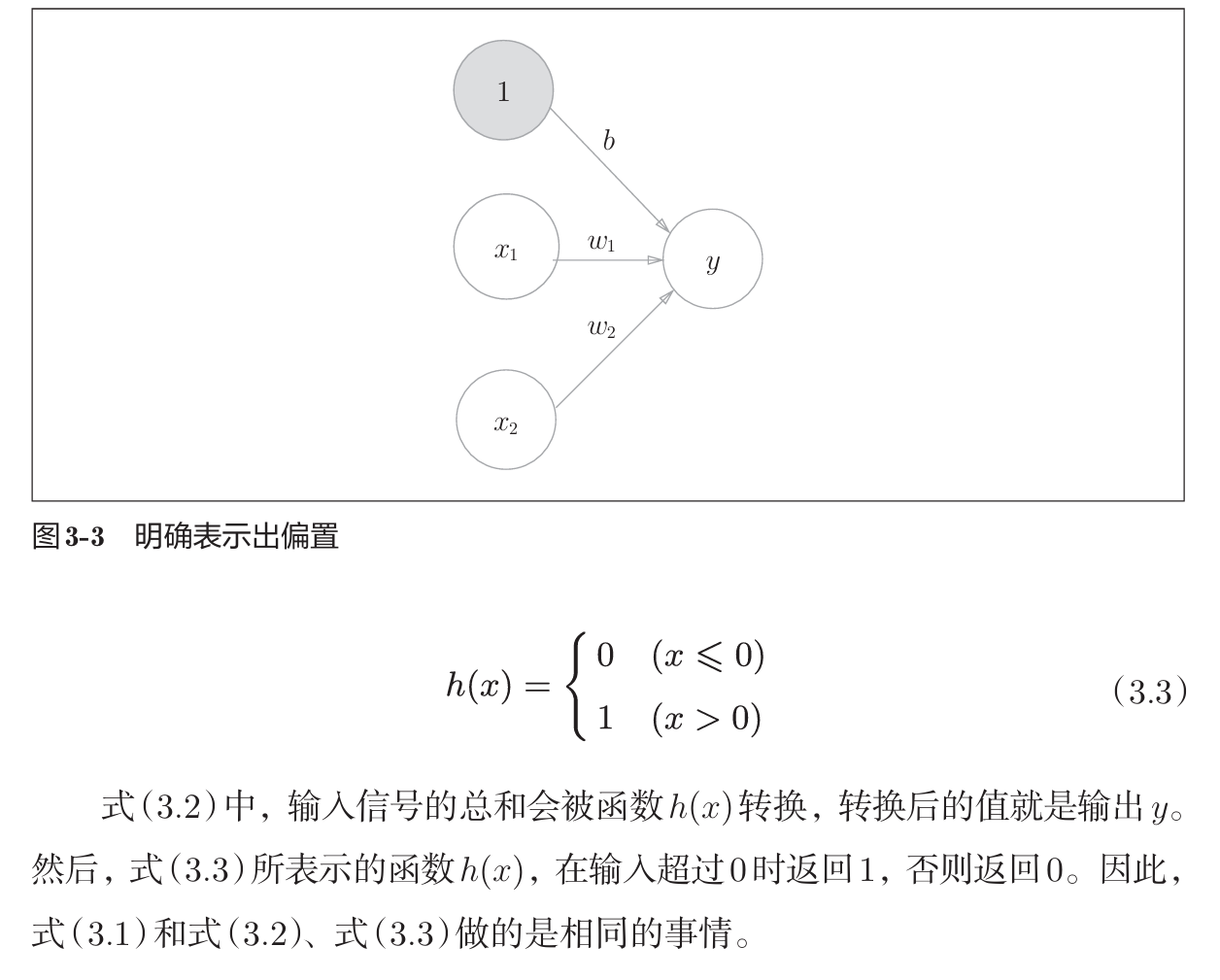
image-20250723132608327

如hx所示，激活函数是将输入信号的总和转换为输出信号。

hx这样的激活函数称为阶跃函数（一旦输入超过阈值就切换输出的函数）。

  • sigmoid函数：
1
2

def sigmoid(x):
    return 1 / (1 + np.exp(-x))

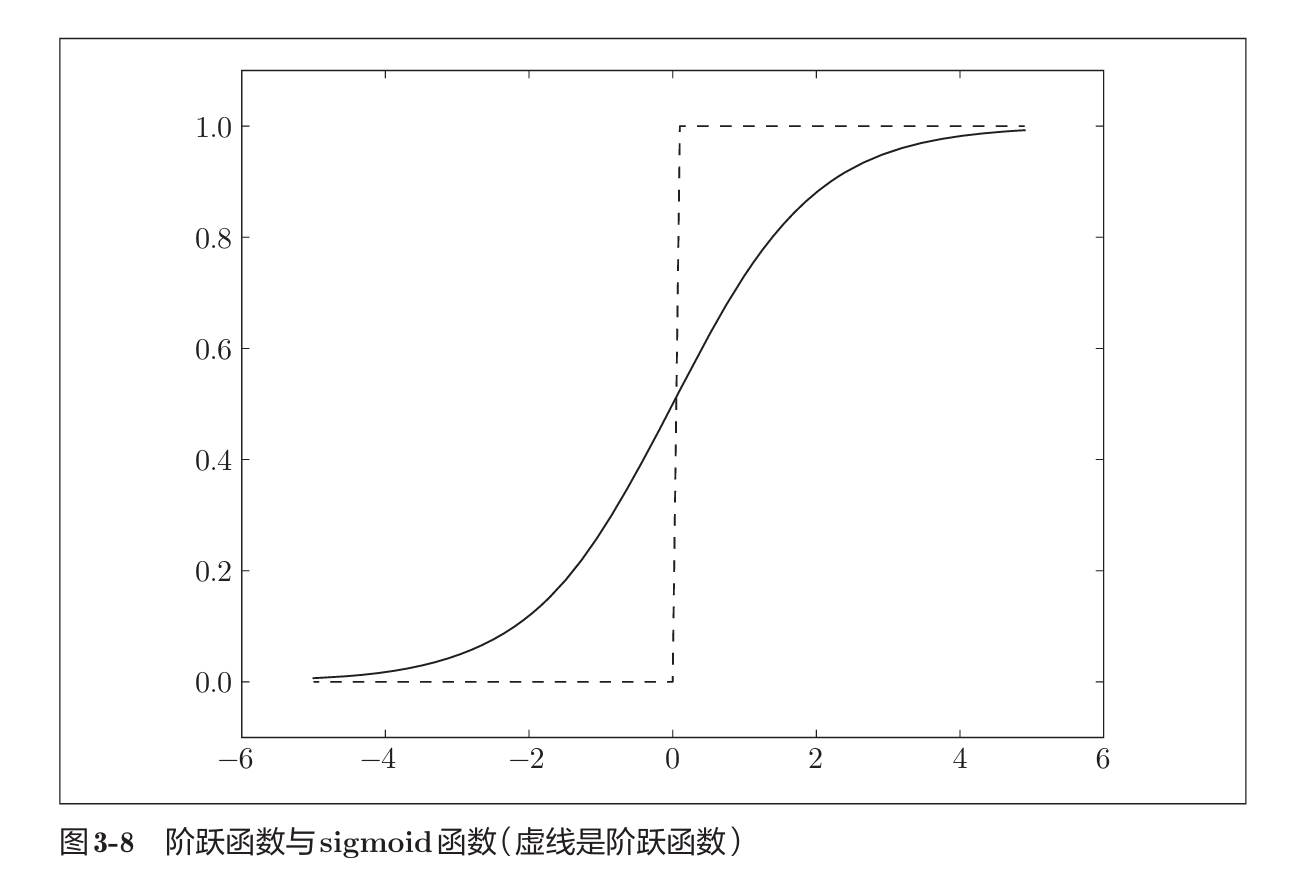
image-20250723133019269

与阶跃函数不同，sigmoid函数1.曲线平滑，2.单调递增，位于(0, 1)中。

神经网络的激活函数必须使用非线性函数，原因在于，线性函数不管如何增加层数，总是存在与之等效的“无隐藏层的神经网络”。

  • ReLU：
1
2
3

def relu(x):
    return np.maximum(0, x)
# 输入大于0时，直接输出该值；在输入小于等于0时，输出0
  • softmax函数

对于分类问题，输出层一般用softmax激活函数；回归问题，输出层一般用恒等函数。

1
2
3
4
5

def softmax(a):
    exp_a = np.exp(a)
    sum_exp_a = np.sum(exp_a)
    y = exp_a / sum_exp_a
    return y

损失函数

  • 均方误差（MSE）：

image-20250723143537419

  • 交叉熵误差：

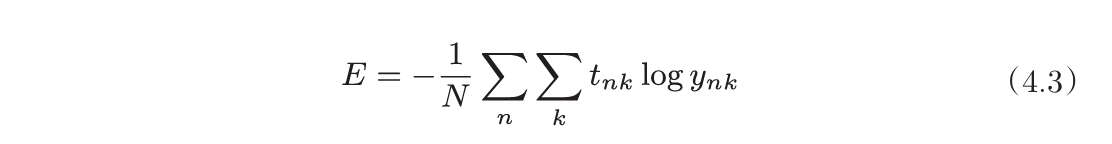
image-20250723162634702

1
2
3
4
5
6
7

def cross_entropy_error(y, t):
    if y.ndim == 1: # 对一维向量[1,2]，转二维统一处理：[[1,2]]
        t = t.reshape(1, t.size)
        y = y.reshape(1, y.size)
    batch_size = y.shape[0]
    return -np.sum(np.log(y[np.arange(batch_size), t] + 1e-7)) / batch_size
# 这里对y取值采用了批量语法，y[第一维取值数组A，第二维取值数组B]，会返回一个新数组，每个元素索引按AB对应的数字取

  • 梯度：模型全部参数的偏导数汇总而成的向量，其单个值是将其他参数值先固定，然后对该参数求偏导数得到，代表了当该参数稍微变化时，损失函数Loss会发生多大变化。

    在求出梯度后，根据学习率*偏导数更新参数

矩阵&向量求导

https://zhuanlan.zhihu.com/p/263777564

本质就是 f 中的每个f分别对变元中的每个元素逐个求偏导，只不过写成了向量、矩阵形式而已。

举几个例子：

  1. 标量f对向量求导，如Loss是均方误差，y是结果向量（一般是一维列向量），最终求导结果是y-t（y，t均为向量）

  2. 矩阵f对矩阵求导，如线性层Y=XW，X(100,784) W(784,50) Y(100,50)，这里直接有结论：

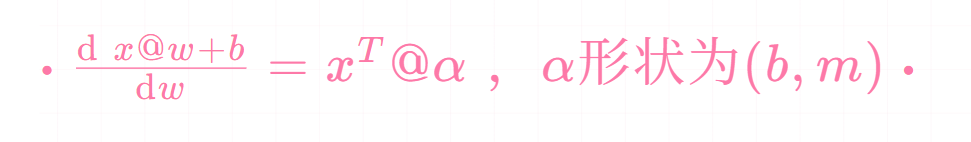
    image-20250724154328191

这里Alpha为全1矩阵，在反向传播过程中，Alpha形状和Y相同，因此我们直接×反向传过来的Y的梯度值即可

https://juejin.cn/post/7325259560524136499

维度验证角度看矩阵求导：

https://zhuanlan.zhihu.com/p/25202034

反向传播

  • 数值微分法：与反向传播更新梯度不同，数值微分法直接采用f(x+h)-f(x-h)/2h的方法进行拟合计算，这样不涉及局部计算，对任意参数（如矩阵W，b），都可以直接用Loss作为f，进行数值微分计算。
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

def numerical_gradient(f, x):
    h = 1e-4  # 扰动步长（避免浮点数精度问题，取 0.0001）
    grad = np.zeros_like(x)  # 初始化梯度数组（与 x 形状相同）
    
    # 遍历 x 的每个元素（支持多维数组）
    it = np.nditer(x, flags=['multi_index'], op_flags=['readwrite'])
    while not it.finished:
        idx = it.multi_index  # 当前元素的多维索引（如 (0,1) 表示第0行第1列）
        
        # 计算 f(x+h)
        tmp_val = x[idx]  # 保存原始值
        x[idx] = float(tmp_val) + h  # 加扰动 h
        fxh1 = f(x)  # 计算函数值
        
        # 计算 f(x-h)
        x[idx] = tmp_val - h  # 减扰动 h
        fxh2 = f(x)  # 计算函数值
        
        # 中心差分法计算梯度
        grad[idx] = (fxh1 - fxh2) / (2*h)
        
        x[idx] = tmp_val  # 恢复原始值（避免影响后续计算）
        it.iternext()  # 移动到下一个元素
        
    return grad

而反向传播法则利用链式法则，大大减少了计算量（之前为了算梯度，还得再前向两次）。

手撸2层神经网络

期望以MNIST数据集为案例，使用numpy手写网络来实现数字识别，可参考鱼书。

https://github.com/jimmie-wang/deep_learning_basic_jim

优化方法

梯度如何更新

在梯度更新的方法中，我们之前用了SGD，随机梯度下降法，其方法简单，但存在如下问题：

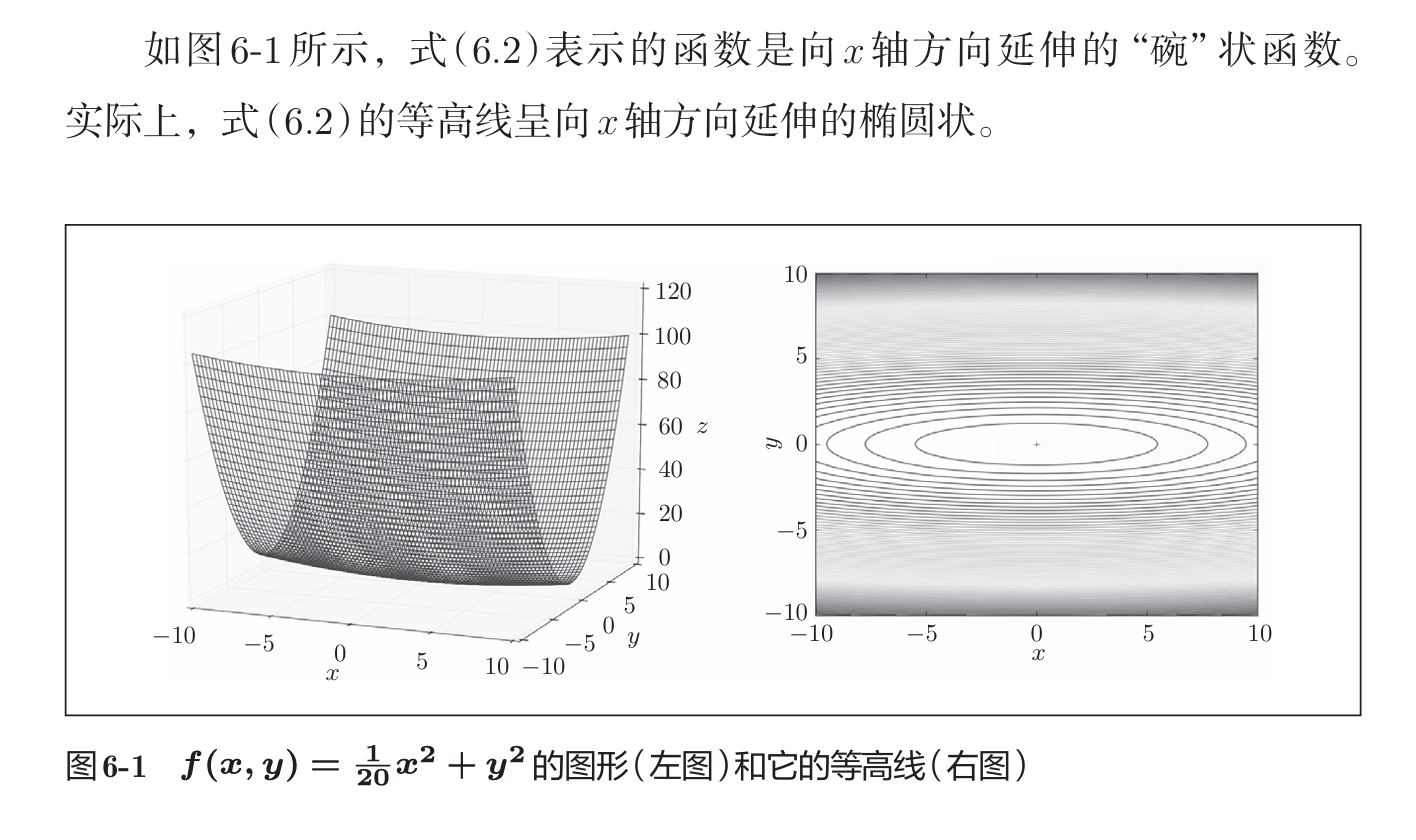
image-20250724193231631

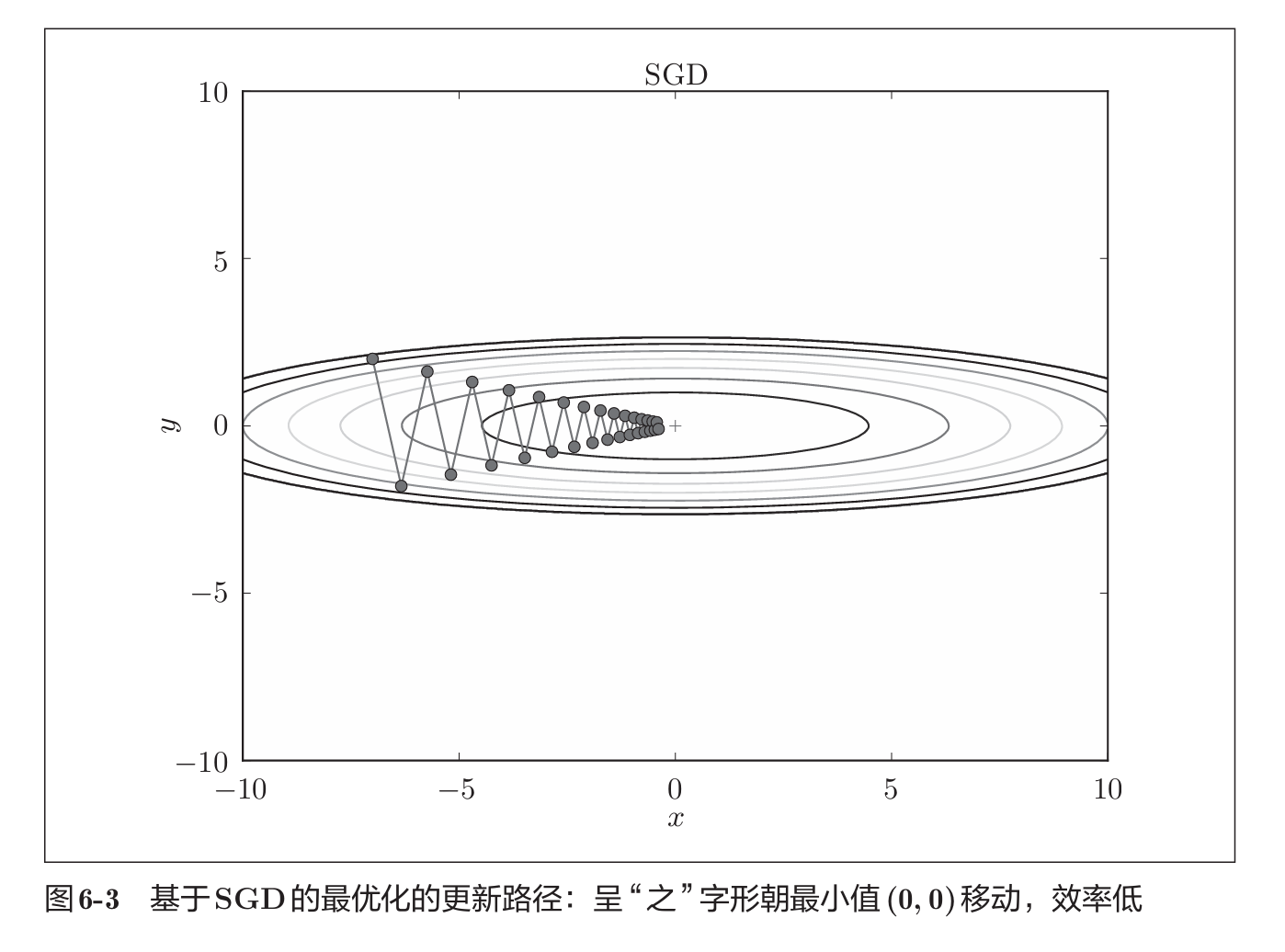
image-20250724193215102

接下来提出几种优化方法改正这一缺点：

  • Momentum：在随机梯度下降基础上，添加之前梯度的影响：

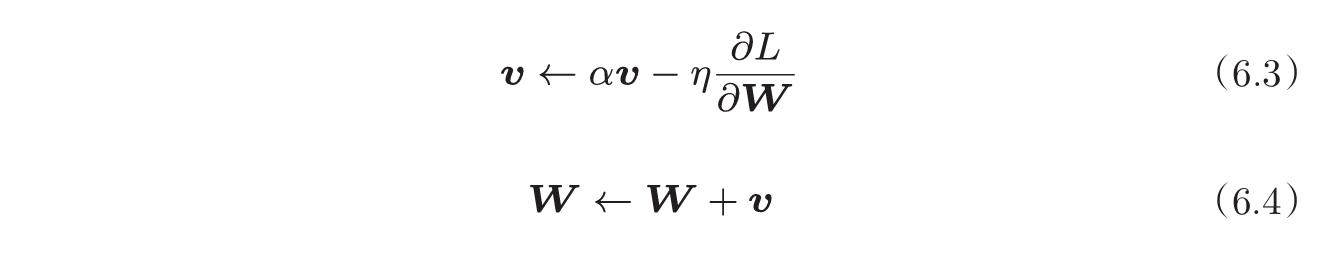
image-20250724194020152

  • AdaGrad：为每个参数，指定逐渐减小的学习率

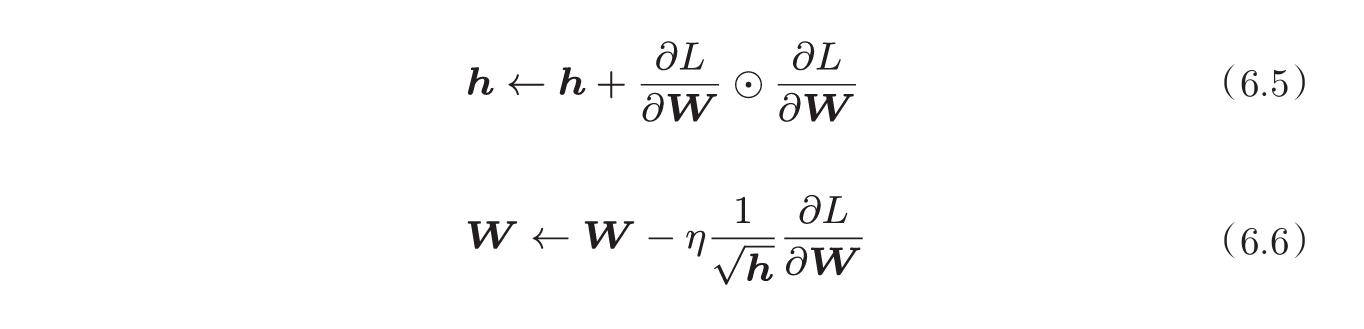
image-20250724194230210

  • Adam：综合了上述两种方法，一个是按照物理规律参考之前运动轨迹，另一个是学习率逐渐衰减。

权重初始值

  • 采用标准差为1的高斯分布，观察激活后值的分布发现，发生了梯度消失；而采用标准差为0.01的高斯分布，发现激活值集中分布在0.5，意味着多个神经元输出几乎相同的值，表现力受限。

  • 当激活函数使用ReLU时，权重初始值使用He初始值，当 激活函数为sigmoid或tanh等S型曲线函数时，初始值使用Xavier初始值。 这是目前的最佳实践。

  • Batch Normalization：调整各层的激活值分布使其拥有适当的广度，在激活函数前，Affine层之后，加入Batch Norm层，将输入数据调整为均值为0，方差为1的分布。通过使用Batch Normalization，可以在训练时不过分依赖初始值。

  • 正则化：

​ 1. 权值衰减，在学习过程中，对大的权重进行惩罚，来抑制过拟合。很多过拟合是由于权重参数取值过大才发生的。通常，我们为损失函数加上权重的平方范数：1/2（lambdaW^2），求导后变为lambdaW。对于所有权重，权值衰减方法都会为损失函数加上1/2（lambda*W^2）。因此，在求权重梯度的计算中，要为之前的误差反向传播法的结果加上正则化项的导数λW。

​ 2.Dropout，在学习过程中，随机删除神经元。

  • 超参数最优化：给超参数设定一个取值范围，并随机取样进行学习，挑出Accuracy较高的取值，并缩小取值范围，不断优化超参数的取值。

卷积神经网络

卷积计算

  • 2维：

卷积核，又称滤波器，在原始图像（假设是m*n的二维数据）上进行矩阵按元素乘法，并移动，输出矩阵后，再加固定偏置。

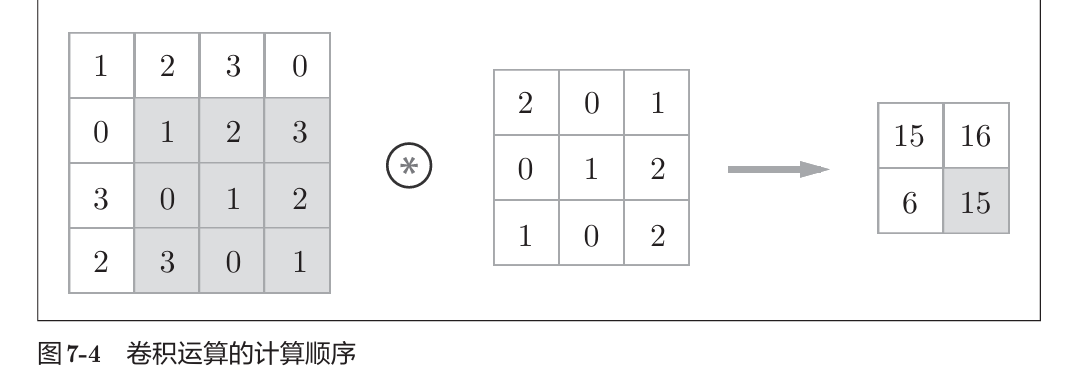
image-20250726154854429

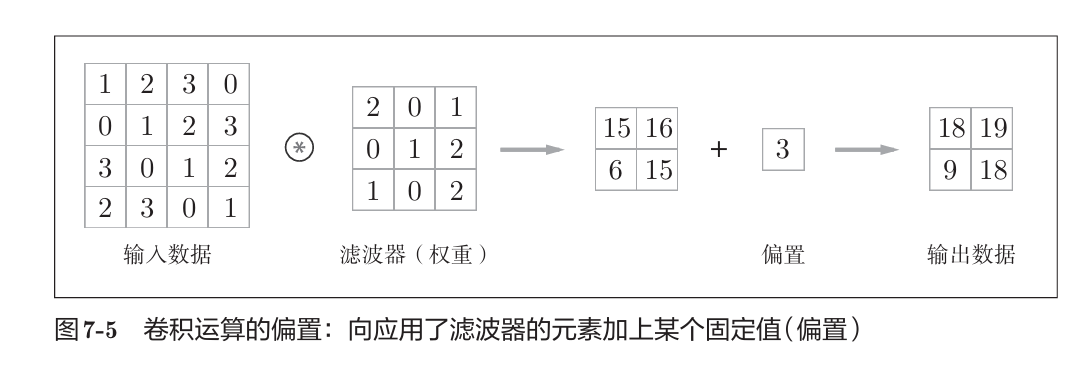
image-20250726154903669

在这个过程中，可能有填充：

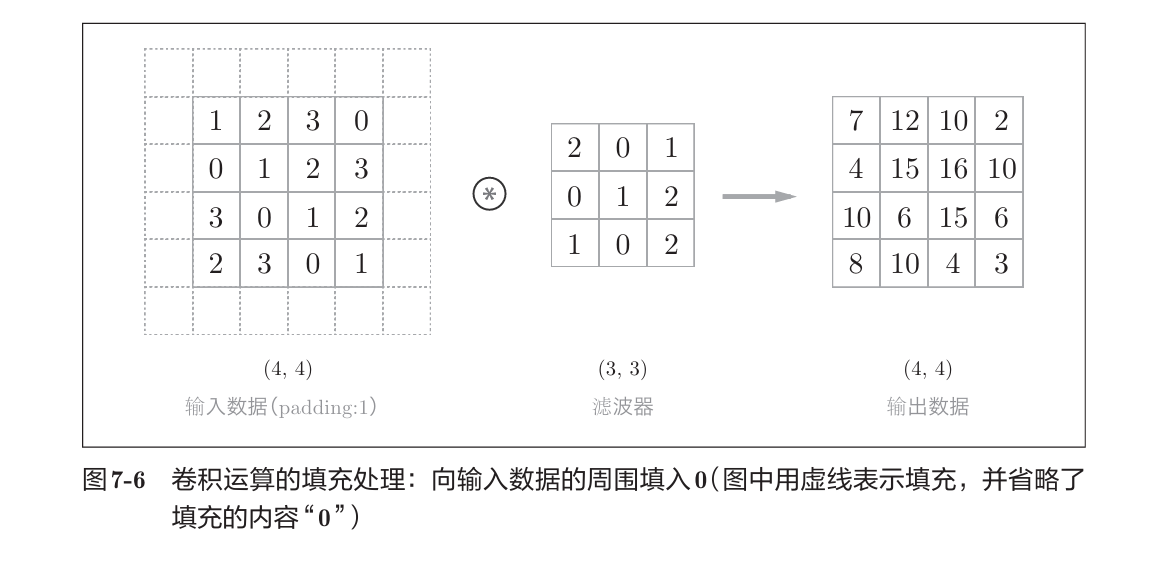
image-20250726154932589

而步幅stride表示每次移动多少单位

由于图像都是三维数据，且需要三个通道结合才能提取出共性特征，因此我们需要三维卷积：

在多通道（维）卷积中，有几个卷积核，结果就有几个通道。如一个卷积核过程：按通道，按元素位置对应取乘积，再相加。

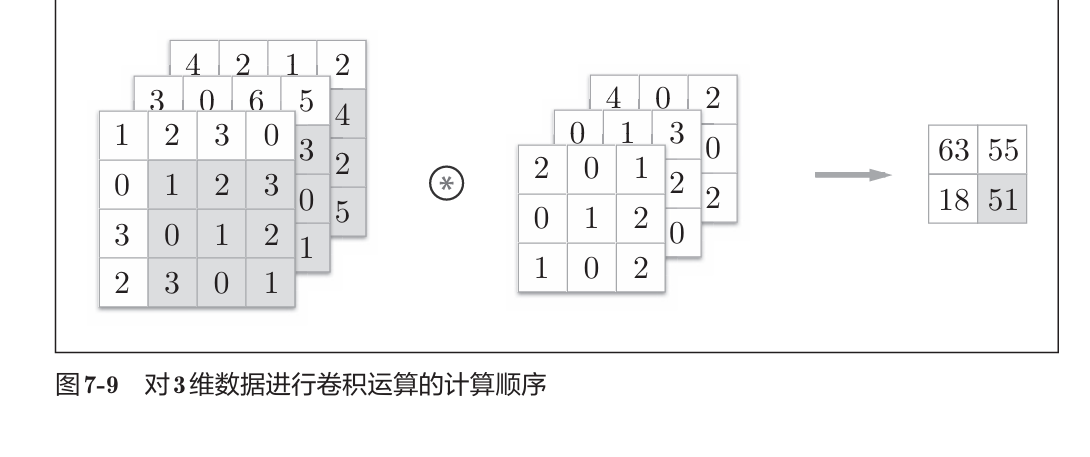
image-20250726155152015

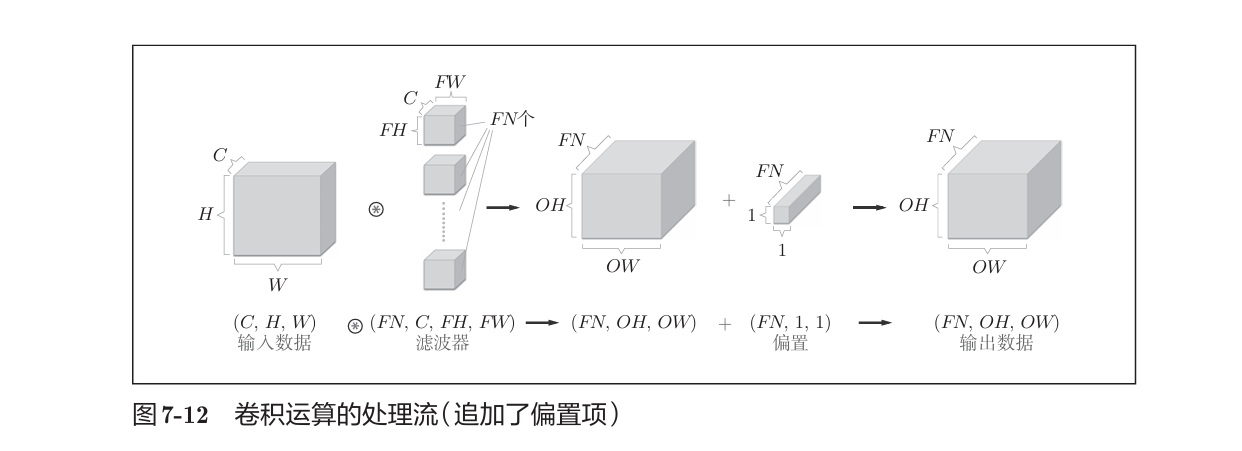
image-20250726155254472

池化计算

缩小高、长方向的空间的运算，有：max池化、average池化

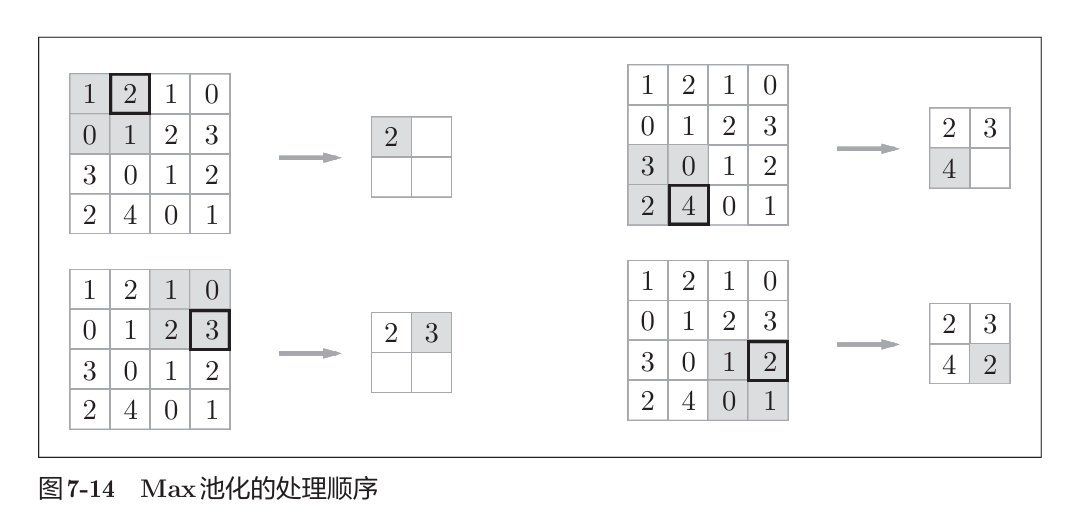
image-20250726155419672

卷积与池化的实现

  • 卷积：传递(N, C, H,W)

为了避免多层for对卷积进行运算，这里基于im2col函数进行展开，之后按照矩阵乘法运算：

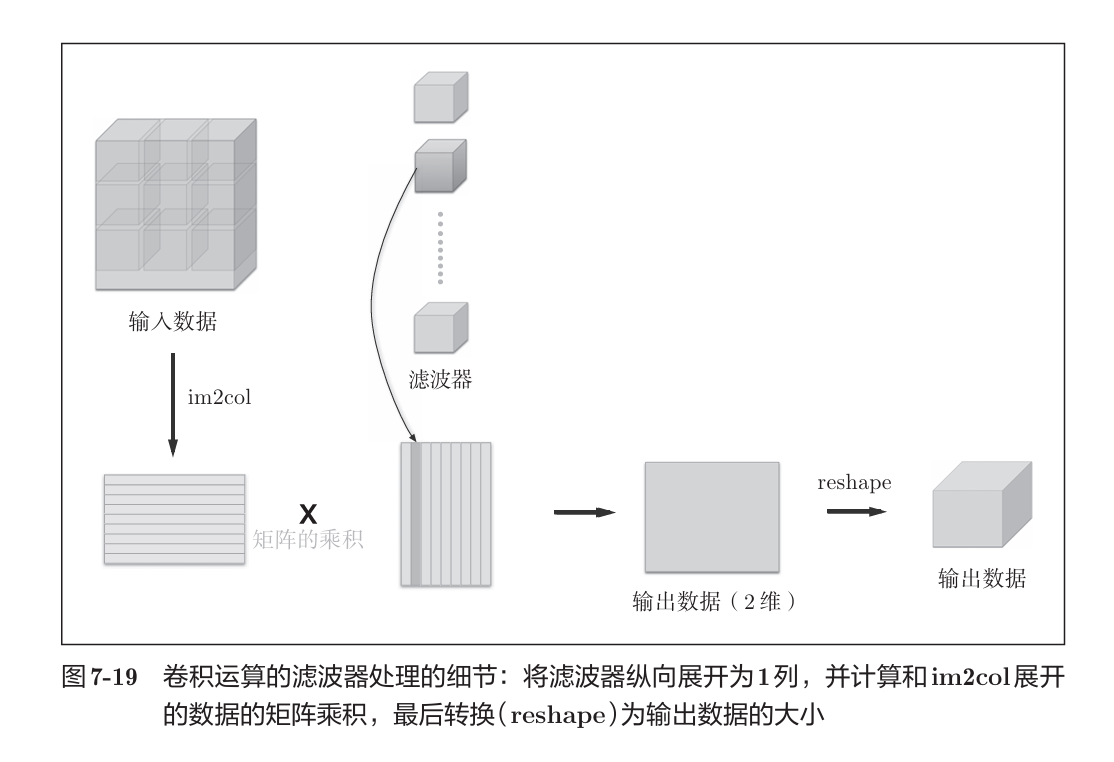
image-20250726155910370

由于一个卷积核输出结果里的一个通道，因此 矩阵的乘积，2维数据中同一列的元素都是一个通道的。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17

class Convolution:
    def __init__(self, W, b, stride=1, pad=0):
        self.W = W
        self.b = b
        self.stride = stride
        self.pad = pad
    def forward(self, x):
        FN, C, FH, FW = self.W.shape
        N, C, H, W = x.shape
        out_h = int(1 + (H + 2*self.pad - FH) / self.stride)
        out_w = int(1 + (W + 2*self.pad - FW) / self.stride)
        col = im2col(x, FH, FW, self.stride, self.pad)
        col_W = self.W.reshape(FN, -1).T # 滤波器的展开
        out = np.dot(col, col_W) + self.b
        out = out.reshape(N, out_h, out_w, -1).transpose(0, 3, 1, 2)
        # transpose，数字表示，原来的第三维数据，放到第二维，原来的第一维放到三，第二维放到4，就是把最后一维，通道数，放到了第二维，使得输出形状符合(N,C,H,W)
        return out
  • 池化：和卷积类似，先通过im2col展开，然后按照池化窗口大小分组，并求最大/平均，最后组装维度
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22

class Pooling:
    def __init__(self, pool_h, pool_w, stride=1, pad=0):
        self.pool_h = pool_h
        self.pool_w = pool_w
        self.stride = stride
        self.pad = pad
    def forward(self, x):
        N, C, H, W = x.shape
        out_h = int(1 + (H - self.pool_h) / self.stride)
        out_w = int(1 + (W - self.pool_w) / self.stride)
        # 
展开(1)
        col = im2col(x, self.pool_h, self.pool_w, self.stride, self.pad)
        col = col.reshape(-1, self.pool_h*self.pool_w)
        # 
最大值(2)
        out = np.max(col, axis=1) # 求完最大，就是一维向量，表示各个最大值
        # 
转换(3)
        out = out.reshape(N, out_h, out_w, C).transpose(0, 3, 1, 2)
        return out # reshape，先按N分，再按out_h即高度是几行，然后再按out_w，每个高度下，能分几列，按顺序分出来，最后是各个通道排序，符合卷积层计算逻辑。最终需要将C通道提前。
© 2025 JimmyWang
网站总访客数：Loading
网站总访问量：Loading
使用 Hugo 构建
主题 Stack 由 Jimmy 设计